Creating Pre-emphasis Audio CD (CD-R, technically)

Creating FIR filter coefficients of pre-emphasis

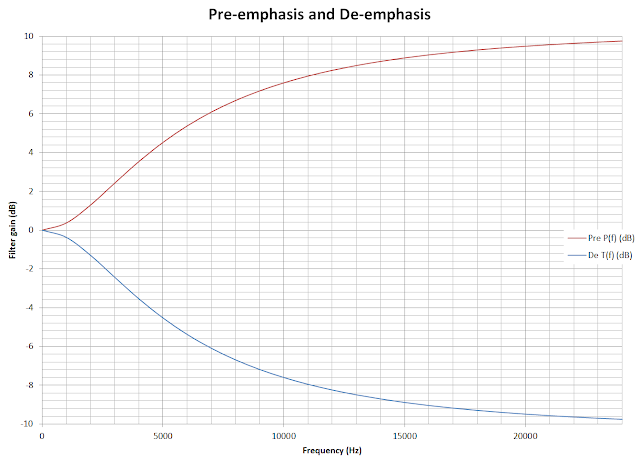
Pre-emphasis frequency  response $P_{\mathrm{dB}}(\mathit{f})=-T_{\mathrm{dB}}(\mathit{f})$ for all frequencies $f$.
$-{\log }_{10}x={\log }_{10}\left(\left(\frac{1}{x}\right)\right)$ therefore

De-emphasis $T_{\mathrm{dB}}(\mathit{f})=10{\log }_{10}\left(\left(\frac{1+\frac{1}{{(0.000015·2\mathit{\pi }\mathit{f})}^2}}{1+\frac{1}{{(0.00005·2\mathit{\pi }\mathit{f})}^2}}\right)\right)-10.4576\dots \dots (1)$
$\mathit{f}:\; frequency\; (Hz)$
$T_{\mathrm{dB}}(\mathit{f})\; :\; De-emphasis\; filter\; gain\; (dB)$

Pre-emphasis $P_{\mathrm{dB}}(\mathit{f})=10{\log }_{10}\left(\left(\frac{1+\frac{1}{{(0.00005·2\mathit{\pi }\mathit{f})}^2}}{1+\frac{1}{{(0.000015·2\mathit{\pi }\mathit{f})}^2}}\right)\right)+10.4576\dots \dots (2)$
$\mathit{f}:\; frequency\; (Hz)$
$P_{\mathrm{dB}}(\mathit{f})\; :\; Pre-emphasis\; filter\; gain\; (dB)$

Note: Math equations of this article uses MathML and it seems it is displayed correctly only on Firefox (as of November 2020).

Now we have frequency response equation of pre-emphasis (2) and FIR filter coefficients can be calculated from  (2) using frequency sampling method, which is explained on the previous article.

Burning Audio CD-R with pre-emphasis

I used Windows PC for the following tasks.

 

Prepare Audio tracks with pre-emphasised

Prepare sound tracks of our Audio CD. 

PCM should be pre-emphasis filtered 44.1kHz 16bit WAV.

• If PCM sample rate is not 44.1kHz or audio file format is not FLAC, convert it to 44.1kHz FLAC using Audacity. https://www.audacityteam.org/download/
  
• Perform pre-emphasis to 44.1kHz 16bit or 24bit FLAC file using sox or FIRFilterConsole https://sourceforge.net/p/playpcmwin/wiki/FIRFilterConsole/
  
• Then the files should be converted from FLAC to 44.1kHz 16bit 2ch WAV using Audacity.

 I prepared the CD track WAV files Track01.wav and Track02.wav on C:\audio folder.

 

Install Cygwin and cdrecord

Download and run Cygwin setup-x86_64.exe https://www.cygwin.com/ 

Install cdrecord package: On the Select Packages menu on the Cygwin installer, Set View to "Full" and input "cdr" to Search. cdrecord package will be shown. On the pulldown list of the New column, select cdrecord version number to install.

Burn Pre-emphasis Audio data to CD-R 

Connect CD-R, DVD-R or BD-RW drive to the computer and insert CD-R.

Start → Cygwin → Cygwin64 Terminal.

Change current directory to C:\audio . Type the following text on the Cygwin64 Terminal :

$ cd /cygdrive/c/audio

Then type ls to show the file list of C:\audio folder. Make sure your wav files are there.

Create Audio CD with pre-emphasis:

$ cdrecord -audio -preemp Track01.wav Track02.wav

View Burned Audio CD-R track info using Exact Audio Copy

It seems Pre-emp is "Yes" 😄

Reading Channel status bit of S/PDIF signal from CD player

Inserted created pre-emphasis CD-R to a CD transport and played. And watched its S/PDIF signal using RME Fireface UC and found emphasis flag of channel status is "None". This means the CD transport de-emphasised PCM signal in digital domain and no further de-emphasis is necessary on receiver/DAC. 

It is possible to de-emphasis pre-emphasised PCM signal by playing it on the CD transport and recording S/PDIF signal using PCM recorder.

Pre-emphasis FIR Filter coefficients of 27 taps

This FIR filter is for 44.1kHz PCM.

-0.0001031041010544631,
3.9223988214258376E-05,
-0.00035340551190767011,
8.1196136261327267E-05,
-0.00091024157376404236,
-0.00022270417890876693,
-0.0025945766943699933,
-0.0022553226067039134,
-0.009562843431584811,
-0.015097813965845558,
-0.051492871033445048,
-0.11992388565207374,
-0.44071105358364959,
2.2862148044176558,
-0.44071105358364959,
-0.11992388565207374,
-0.051492871033445048,
-0.015097813965845558,
-0.009562843431584811,
-0.0022553226067039134,
-0.0025945766943699933,
-0.00022270417890876693,
-0.00091024157376404236,
8.1196136261327267E-05,
-0.00035340551190767011,
3.9223988214258376E-05,
-0.0001031041010544631,


Filtering sound files using sox

The following examples inputs 44.1kHz PCM file inFile.flac and apply 27taps Pre-emphasis FIR filter and output it as outFile.flac (this filter increases gain so sample value overflow may occur):

sox inFile.flac outFile.flac fir -0.0001031041010544631 3.9223988214258376E-05 -0.00035340551190767011 8.1196136261327267E-05 -0.00091024157376404236 -0.00022270417890876693 -0.0025945766943699933 -0.0022553226067039134 -0.009562843431584811 -0.015097813965845558 -0.051492871033445048 -0.11992388565207374 -0.44071105358364959 2.2862148044176558 -0.44071105358364959 -0.11992388565207374 -0.051492871033445048 -0.015097813965845558 -0.009562843431584811 -0.0022553226067039134 -0.0025945766943699933 -0.00022270417890876693 -0.00091024157376404236 8.1196136261327267E-05 -0.00035340551190767011 3.9223988214258376E-05 -0.0001031041010544631

Designing De-emphasis Digital Filter for old CDs Part 3: Using Reference Equation

 There is a reference de-emphasis equation on this page (Thanks miguelito-san) : https://forums.stevehoffman.tv/threads/cd-dat-with-pre-emphasis-how-to-de-emphasize-correctly.88541/

$T_{\mathrm{dB}}(\mathit{f})=10{\log }_{10}\left(\left(\frac{1+\frac{1}{{(0.000015·2\mathit{\pi }\mathit{f})}^2}}{1+\frac{1}{{(0.00005·2\mathit{\pi }\mathit{f})}^2}}\right)\right)-10.4576\dots \dots (1)$
$\mathit{f}:\; frequency\; (Hz)$
$T_{\mathrm{dB}}(\mathit{f})\; :\; De-emphasis\; filter\; gain\; (dB)$

This decibel is root power quantity therefore actual gain magnitude value T(f) is:

$\mathit{f}:\; frequency\; (Hz)$
$T(\mathit{f})\; :\; De-emphasis\; filter\; gain\; magnitude\; value\; at\; frequency\mathit{f}$

Note 1: Math equations of this article uses MathML and it seems it is displayed correctly only on Firefox (as of November 2020).

Note 2: It seems 0.00005 and 0.000015 of equation 1 means 50 microseconds and 15 microseconds respectively and it is called 50/15 microsec emphasis.

On this article, equation (2) is used to create frequency sampling FIR digital filter.

Calculation steps are very similar to Part 2.

Example : Calculation of M=9 taps FIR filter coeffs using equation $T(\mathit{f})$

When sampling frequency==44100 Hz and Desired FIR filter taps M==9,

Frequency sampling index $k=0,1,2,\; ..,\frac{M-1}{2}=4$

$k\; =\; 0,\; 1,\; 2,\; 3\; and\; 4$

Frequency sampling angle frequency ${\omega }_{\mathrm{k}}=\frac{2\pi k}{M}:$

• $k\; =\; 0\; :\; {\omega }_0=\; 0,\; freq0\; =\; 0\; Hz$
  
• $k\; =\; 1\; :\; {\omega }_1=\; 2\pi /9,\; freq1\; =\; (44100/2\pi )(2\pi /9)\; =\; 44100\; /\; 9\; Hz\; =\; 4900\; Hz$
• $k\; =\; 2\; :\; {\omega }_2=\; 4\pi /9,\; freq2\; =\; (44100/2\pi )(4\pi /9)\; =\; 44100\; *\; 2\; /\; 9\; Hz\; =\; 9800\; Hz$
• $k\; =\; 3\; :\; {\omega }_3=\; 6\pi /9,\; freq3\; =\; (44100/2\pi )(6\pi /9)\; =\; 44100\; *\; 3\; /\; 9\; Hz\; =\; 14700\; Hz$
• $k\; =\; 4\; :\; {\omega }_4=\; 8\pi /9,\; freq4\; =\; (44100/2\pi )(8\pi /9)\; =\; 44100\; *\; 4\; /\; 9\; Hz\; =\; 19600\; Hz$

Get filter gain on those frequencies $Hr({\omega }_{\mathrm{k}})$ using Equation (2):

• $Hr($ {\omega }_0)\; =\; T(0)\; =\; 1$$
• $Hr($ {\omega }_1)\; =\; T(4900)\; =\; 0.60004356$$
• $Hr($ {\omega }_2)\; =\; T(9800)\; =\; 0.420524967$$
• $Hr($ {\omega }_3)\; =\; T(14700)\; =\; 0.361602897$$
• $Hr($ {\omega }_4)\; =\; T(19600)\; =\; 0.336724814$$

Then G(k) is calculated from $Hr({\omega }_{\mathrm{k}})$ by $G(k)\; ={\mathrm{(-1)}}^{\mathrm{k}}Hr($ {\omega }_{\mathrm{k}})\; \dots \dots (3)\; :$$

• $G(0)\; ={\mathrm{(-1)}}^{0}Hr($ {\omega }_0)\; =\; 1$$
• $G(1)\; ={\mathrm{(-1)}}^{1}Hr($ {\omega }_1)\; =\; -0.60004356$$
• $G(2)\; ={\mathrm{(-1)}}^{2}Hr($ {\omega }_2)\; =\; 0.420524967$$
• $G(3)\; ={\mathrm{(-1)}}^{3}Hr($ {\omega }_3)\; =\; -0.361602897$$
• $G(4)\; ={\mathrm{(-1)}}^{4}Hr($ {\omega }_4)\; =\; 0.336724814$$

FIR filter coefficients h(n) can be calculated by $h(n)\; =\frac{1}{M}\left\{G(0)+2\sum _{\mathrm{k=1}}^{\mathrm{(M-1)/2}}G(k)cos\frac{2\pi k(n+1/2)}{M}\right\}\dots (4)$

• $h(0)\; =\; 0.030212113446082472$
• $h(1)\; =\; 0.040656939222222181$
• $h(2)\; =\; 0.063594885887469199$
• $h(3)\; =\; 0.11899203499978166$
• $h(4)\; =\; 0.49308805288888891$

Finally, this FIR filter is symmetry (linear phase), therefore h(8) = h(0), h(7) = h(1), h(6) = h(2), h(5) = h(3).

• $h(0)\; =\; 0.030212113446082472$
• $h(1)\; =\; 0.040656939222222181$
• $h(2)\; =\; 0.063594885887469199$
• $h(3)\; =\; 0.11899203499978166$
• $h(4)\; =\; 0.49308805288888891$
• $h(5)\; =\; 0.11899203499978166$
• $h(6)\; =\; 0.063594885887469199$
• $h(7)\; =\; 0.040656939222222181$
• $h(8)\; =\; 0.030212113446082472$

We've got all the 9 FIR filter coefficients h(n).

Evaluating Frequency Response of FIR filter

Now one FIR filter is available for testing. FIR filter gain of arbitrary angular frequency ω can be calculated using the following equation:

$Gain(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)e^{\mathrm{-jk\omega }}\dots \dots (5)$

Real part and imaginary part of (5) can be calculated separately:

${\mathrm{Gain}}_{\mathrm{real}}(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)cos(-k\omega )\; \dots \dots (5r)$
${\mathrm{Gain}}_{\mathrm{imaginary}}(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)sin(-k\omega )\; \dots \dots (5i)$

And FIR filter Gain magnitude is calculated as follows:

Finally Gain in decibel is: ${\mathrm{Gain}}_{\mathrm{dB}}(\omega )\; =\; 20{\log }_{10}\left\{{\mathrm{Gain}}_{\mathrm{magnitude}}(\omega )\right\}\dots \dots (7)$

For our M=9 FIR filter, frequency response can be calculated using equation (7). And this time reference equation is available: desirable gain of any frequency can be calculated, it is possible to compare gain values at as many frequency points as you wish. I compared 10Hz to 22040Hz semitone step frequency points and created Fig.1.

Fig.1. 9 taps FIR de-emphasis filter frequency response.

Comparing to the original de-emphasis table, max error of this FIR filter is 0.878 dB on 7360Hz, It is poor, and the quality can be improved by increasing M.

Searching the best FIR filter tap number M

FIR Filter Taps M	Max Error (dB)
9	0.878
15	0.1704
17	0.115
19	0.0631
21	0.0522
23	0.0231
25	0.0272
27	0.00882

Table 1: FIR Filter taps and max error 

Fig.2 : Frequency Response of FIR Filter, taps=19  note: frequency axis is logarithmic.

Fig.3 : Frequency Response of FIR Filter, taps=27  note: frequency axis is logarithmic.

Fig.4 : Gain Error of FIR Filter, taps=27

De-emphasis FIR Filter Coefficients for 44.1kHz PCM data

19taps linear-phase FIR filter coefficients h(n) of max error = 0.0631 dB is as follows:

0.0022333652179533105,
0.0027676001211334594,
0.0042218013139663415,
0.0065438712761329912,
0.011312237381544295,
0.01877355043394098,
0.03398288954901494,
0.059120380386441337,
0.11593361915957012,
0.49022137032060437,
0.11593361915957012,
0.059120380386441337,
0.03398288954901494,
0.01877355043394098,
0.011312237381544295,
0.0065438712761329912,
0.0042218013139663415,
0.0027676001211334594,
0.0022333652179533105,

27taps linear-phase FIR filter coefficients h(n) of max error = 0.00882 dB is as follows:

0.00031102739649091732,
0.00036885685453166665,
0.00057659816229764602,
0.00082952248115418167,
0.001449970925925961,
0.0022387507393955598,
0.0039420948394406248,
0.0063363475292175873,
0.011215231698621361,
0.018685854350970088,
0.033951734838472802,
0.059076192885731141,
0.11592376177923121,
0.49018811103703697,
0.11592376177923121,
0.059076192885731141,
0.033951734838472802,
0.018685854350970088,
0.011215231698621361,
0.0063363475292175873,
0.0039420948394406248,
0.0022387507393955598,
0.001449970925925961,
0.00082952248115418167,
0.00057659816229764602,
0.00036885685453166665,
0.00031102739649091732,

Filtering sound files using sox

With sox, it is possible to use those coefficients to filter the 44.1kHz PCM sound files. The following examples inputs inFile.flac and apply 27taps De-emphasis FIR filter and output it as outFile.flac:

sox inFile.flac outFile.flac fir 0.00031102739649091732 0.00036885685453166665 0.00057659816229764602 0.00082952248115418167 0.001449970925925961 0.0022387507393955598 0.0039420948394406248 0.0063363475292175873 0.011215231698621361 0.018685854350970088 0.033951734838472802 0.059076192885731141 0.11592376177923121 0.49018811103703697 0.11592376177923121 0.059076192885731141 0.033951734838472802 0.018685854350970088 0.011215231698621361 0.0063363475292175873 0.0039420948394406248 0.0022387507393955598 0.001449970925925961 0.00082952248115418167 0.00057659816229764602 0.00036885685453166665 0.00031102739649091732

Next article: Creating Pre-emphasis Audio CD

Designing De-emphasis Digital Filter for Old CDs Part 2 : Frequency Sampling Method

On the previous blog post, we've got a 6th degree polynomial function of de-emphasis curve Equation 1:

$f\mathrm{dB}(x)\; =\; -0.0000029212346025337816x^6+0.00020291497408909238x^5-0.0054888099286801205x^4+0.071110615465301924x^3-0.40078216359333169x^2-0.11354738870338571x$

$x\; :\; frequency\; (kHz)$
$f_{\mathrm{dB}}(x):\; filter\; gain\; (dB)$

Note: Math equations of this article uses MathML and it seems it is displayed correctly only on Firefox (as of November 2020).

This decibel is root power quantity therefore actual gain value f(x) is:

Next step is to create filter gain table of equal spacing frequency using this function.

And create the filter, evaluate its frequency response error from original de-emphasis table and choose the best FIR filter tap number M.

 

Example : Calculation of M=9 taps FIR filter coeffs

When sampling frequency==44100 Hz and Desired FIR filter taps M==9,

Frequency sampling index $k=0,1,2,\; ..,\frac{M-1}{2}=4$

$k=0,1,2,3\; and\; 4$

Frequency sampling angle frequency ${\omega }_{\mathrm{k}}=\frac{2\pi k}{M}:$

• $k=0: {\omega }_0=\; 0, {\mathrm{freq}}_0=\; 0\; Hz$
  
• $k=1: {\omega }_1=\; 2\pi /9, {\mathrm{freq}}_1=\; (44100/2\pi )(2\pi /9)\; =\; 44100\; /\; 9\; Hz\; =\; 4900\; Hz$
• $k=2: {\omega }_2=\; 4\pi /9, {\mathrm{freq}}_2=\; (44100/2\pi )(4\pi /9)\; =\; 44100\; *\; 2\; /\; 9\; Hz\; =\; 9800\; Hz$
• $k=3: {\omega }_3=\; 6\pi /9, {\mathrm{freq}}_3=\; (44100/2\pi )(6\pi /9)\; =\; 44100\; *\; 3\; /\; 9\; Hz\; =\; 14700\; Hz$
• $k=4: {\omega }_4=\; 8\pi /9, {\mathrm{freq}}_4=\; (44100/2\pi )(8\pi /9)\; =\; 44100\; *\; 4\; /\; 9\; Hz\; =\; 19600\; Hz$

Get filter gain on those frequencies $Hr({\omega }_{\mathrm{k}})$ using Equation (2):

• $Hr({\omega }_0)\; =\; f(0)\; =\; 1$
• $Hr({\omega }_1)\; =\; f(4.9)\; =\; 0.599479869$
• $Hr({\omega }_2)\; =\; f(9.8)\; =\; 0.419371436$
• $Hr({\omega }_3)\; =\; f(14.7)\; =\; 0.359695479$
• $Hr({\omega }_4)\; =\; f(19.6)\; =\; 0.33620803$

Then G(k) is calculated from $Hr({\omega }_{\mathrm{k}})$ by $G(k)\; ={\mathrm{(-1)}}^{\mathrm{k}}Hr({\omega }_{\mathrm{k}})\; \dots \dots (3)\; :$

• $G(0)\; ={\mathrm{(-1)}}^{0}Hr({\omega }_0)\; =\; 1$
• $G(1)\; ={\mathrm{(-1)}}^{1}Hr({\omega }_1)\; =\; -0.599479869$
• $G(2)\; ={\mathrm{(-1)}}^{2}Hr({\omega }_2)\; =\; 0.419371436$
• $G(3)\; ={\mathrm{(-1)}}^{3}Hr({\omega }_3)\; =\; -0.359695479$
• $G(4)\; ={\mathrm{(-1)}}^{4}Hr({\omega }_4)\; =\; 0.33620803$

FIR filter coefficients h(n) can be calculated by $h(n)\; =\frac{1}{M}\left\{G(0)+2\sum _{\mathrm{k=1}}^{\mathrm{(M-1)/2}}G(k)cos\frac{2\pi k(n+1/2)}{M}\right\}\dots (4)$

• $h(0)\; =\; 0.0303254491484693$
• $h(1)\; =\; 0.0404812914444444$
• $h(2)\; =\; 0.0639379770301665$
• $h(3)\; =\; 0.119171414154698$
• $h(4)\; =\; 0.492167736444444$

And finally, This FIR filter is symmetry shape, therefore h(8) = h(0), h(7) = h(1), h(6) = h(2), h(5) = h(3).

• $h(0)\; =\; 0.0303254491484693$
• $h(1)\; =\; 0.0404812914444444$
• $h(2)\; =\; 0.0639379770301665$
• $h(3)\; =\; 0.119171414154698$
• $h(4)\; =\; 0.492167736444444$
• $h(5)\; =\; 0.119171414154698$
• $h(6)\; =\; 0.0639379770301665$
• $h(7)\; =\; 0.0404812914444444$
• $h(8)\; =\; 0.0303254491484693$

We've got all the 9 FIR coefficient values h(n).

Evaluating Frequency Response of FIR filter

Now one FIR filter coefficients h(n) is available for testing. FIR filter gain of arbitrary angular frequency ω can be calculated using the following equation:

$Gain(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)e^{\mathrm{-jk\omega }}\dots \dots (5)$

Real part and imaginary part of (5) can be calculated separately:

${\mathrm{Gain}}_{\mathrm{real}}(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)cos(-k\omega )\; \dots \dots (5r)$
${\mathrm{Gain}}_{\mathrm{imaginary}}(\omega )\; =\sum _{\mathrm{k=0}}^{\mathrm{M-1}}h(k)sin(-k\omega )\; \dots \dots (5i)$

And FIR filter Gain magnitude is calculated as follows:

Finally Gain in decibel is: ${\mathrm{Gain}}_{\mathrm{dB}}(\omega )\; =\; 20{\log }_{10}\left\{{\mathrm{Gain}}_{\mathrm{magnitude}}(\omega )\right\}\dots \dots (7)$

For our M=9 FIR filter, frequency response can be calculated using equation (7):

Frequency(kHz)	${\mathrm{Gain}}_{\mathrm{dB}}(\omega )$
0	0
1	-0.214929748
2	-0.847460501
3	-1.855702469
4	-3.153141013
5	-4.58835657
6	-5.939107409
7	-6.960958392
8	-7.506314657
9	-7.624120111
10	-7.521831664
11	-7.433783042
12	-7.52486218
13	-7.862458657
14	-8.419180318
15	-9.081142015
16	-9.670162018
17	-10.00514702
18	-9.997371674
19	-9.707880014
20	-9.30607583
21	-8.974681539
22	-8.840811148

Table 1

Comparing to the original de-emphasis table, max error of this FIR filter is 0.87 dB on 7kHz, It is poor and may be M=9 is too small.

Finding Optimal FIR filter taps M

I'd like to have < 0.1 dB error of FIR filter with minimum filter taps. Calculated error from the original table on several M using DesignFrequencySamplingFilter and compared their performance.

Filter taps M	Max error from the original table
9	0.871 dB
17	0.217 dB
19	0.140 dB
21	0.172 dB
23	0.104 dB
25	0.118 dB
27	0.0779 dB
29	0.0802 dB
31	0.0795 dB
33	0.0770 dB

Table 2

From the table 2, M=27 is the most desirable one.

On M=27,  maximum error from the original table is 0.0779 dB on 2kHz.

Resulted linear-phase FIR filter coefficients h(n) of M=27 for 44.1kHz PCM is as follows:

0.00087829953598830856,
0.00073354073461322569,
0.0013059505528472161,
0.00089158366884379073,
0.0022743712962963354,
0.0017509721612062167,
0.0046856769010995523,
0.0049418323357026065,
0.011621996337245248,
0.017825153275235591,
0.034805918374128435,
0.057946349576219941,
0.11652885832464696,
0.48761899385185181,
0.11652885832464696,
0.057946349576219941,
0.034805918374128435,
0.017825153275235591,
0.011621996337245248,
0.0049418323357026065,
0.0046856769010995523,
0.0017509721612062167,
0.0022743712962963354,
0.00089158366884379073,
0.0013059505528472161,
0.00073354073461322569,
0.00087829953598830856

Fig.1 M=27 de-emphasis FIR Filter frequency response

This linear-phase de-emphasis FIR filter is available on DSP menu of PlayPcmWin 5.0.79. Source code is https://sourceforge.net/p/playpcmwin/code/HEAD/tree/PlayPcmWin/WasapiIODLL/WWAudioFilterDeEmphasis.cpp

 

Continued to Part 3 (Improving accuracy): https://yamamoto2002.blogspot.com/2020/11/designing-de-emphasis-digital-filter.html

 

 Reference

 J.G. Proakis & D.G. Manolakis: Digital Signal Processing, 4th edition, 2007, Chapter 10, pp. 671-678

Designing De-emphasis Digital Filter for Old CDs Part 1: Polynomial Fitting

 
I have one pre-emphasis CD and ripped it to FLAC files. In order to play it correctly, de-emphasis is necessary. So started to design de-emphasis filter for 44.1kHz PCM.

There are many ways to design filters. I chose frequency-sampling method to create linear-phase FIR filter.

De-emphasis filter curve

From the following page, there is a frequency response table: https://archimago.blogspot.com/2020/09/how-to-cd-pre-emphasis-and-dealing-with.html

f(Hz)	De-emphasis filter gain (dB)
0	0
1	-0.37
2	-1.29
3	-2.43
4	-3.54
5	-4.53
6	-5.38
7	-6.09
8	-6.69
9	-7.19
10	-7.6
11	-7.95
12	-8.24
13	-8.49
14	-8.71
15	-8.89
16	-9.04
17	-9.18
18	-9.3
19	-9.4
20	-9.49

Table 1 De-emphasis filter frequency response

Polynomial fitting

In order to design the filter, it is necessary to know the filter gain of arbitrary frequency. So I tried Excel polynomial fit to find the best polynomial equation.

Note: this process is not necessary, because reference frequency response function is available: https://yamamoto2002.blogspot.com/2020/11/designing-de-emphasis-digital-filter.html

Fig.1 line fitting

Fig.2 2nd degree polynomial fit

Fig.3 3rd degree polynomial fit

Fig.4 4th degree polynomial fit

Fig.5 5th degree polynomial fit

Fig.6 6th degree polynomial fit

From the graphs above, 6th degree polynomial is the best and I decided to use it. other functions have a problem on the 0Hz～2kHz region, and its frequency band is very important for music. the error can be reduced further by increasing polynomial degree but I think < 0.1 dB is sufficient.

Calculating Polynomial coefficient

Excel shows 6th degree polynomial coefficient values on Fig.6, but it is ballpark values and more precise coefficient values are needed. Polynomial fit code WWPolynomialFit.cs to get 6th polynomial coefficient values.

Result is:

constant	1st	2nd	3rd	4th	5th	6th
0.028327961846712043	-0.11354738870338571	-0.40078216359333169	0.071110615465301924	-0.0054888099286801205	0.00020291497408909238	-0.0000029212346025337816

Table 2. 6th degree polynomial coefficients

There is a very small constant value but it should be 0 to prevent PCM integer overflow, so I just modified constant coefficient to zero.

Resulted equation is:

$y=\; -0.0000029212346025337816x^6+0.00020291497408909238x^5-0.0054888099286801205x^4+0.071110615465301924x^3-0.40078216359333169x^2-0.11354738870338571x\; \dots \dots (1)$
$x\; :\; Frequency\; (kHz)$
$y\; :\; Filter\; gain\; (dB)$

Note: Math equations of this article uses MathML and it seems it is displayed correctly only on Firefox (as of November 2020).

Error from the table values are: 0.079 dB on 1kHz, 0.053 dB on 2kHz, and so on.

Now it is possible to get the filter gain at arbitrary frequency using the equation (1).

Continued to Part 2: https://yamamoto2002.blogspot.com/2020/11/designing-de-emphasis-fir-filter-for.html